2013年12月23日
宝くじというギャンブルの数学的考察

「当たると有名な売り場」ではない有楽町で買いました
みなさん、年末ジャンボ宝くじは買いましたか?
私もこれまで、サマージャンボと年末ジャンボだけは(忘れなければ)購入してきました。
宝くじは「夢を買う」などとよく言われますが、私の場合はまさにそれで、サマージャンボの結果は年末ジャンボを買った時に確認し、年末ジャンボはサマージャンボを買った時に…と、“夢を途切れさせないために”、常に“当たっているかもしれない”宝くじを手もとに置いています。
戦歴はと言えば、遠い昔に、たぶん3千円程度当たったような気もしないではないのですが、それも定かではありません。
そんな「確実に当たらない」宝くじなのに、なぜ買い続けているのでしょうか?
今日は、こうも当たらない宝くじについて、冷静に考えてみたいと思います。
ちょっと長くなりそうですので、興味のない方は斜め読みでどうぞ。

さて、宝くじの当選確率って一体どれくらいのものなのでしょう?
宝くじは買っているのに、果たして1等の当選確率がどれほどのものか、案外知らない方も多いのではないでしょうか。
年に5回あるジャンボ宝くじの1等当選確率は、なんと1000万分の1です。
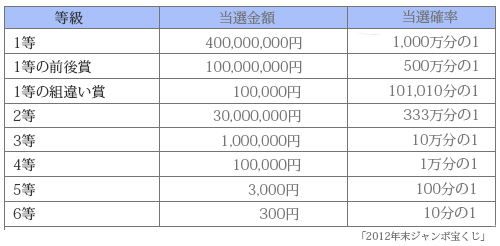
1000万個の球の入った抽選器(ガラガラ)の中に、たった1個の1等の球が入っていることを考えると、これがいかに確率の低いものかおわかりになるかと思います。
よりわかりやすくするために、ガラガラの球の直径が1cmとして計算すると、ぎっしりと球を積んだ10tダンプ約35台分の中に1個という割合です。

一列に並べたら、その距離実に100kmにも及びます。
こんなの当たるわけないよなぁ、という気になってきますよね。
しかし、「1等60本」だとか、「毎回○○名の億万長者が誕生」とかいうCMを見聞きしていると、「…きっと自分も当たるのでは?」という気になってくるから不思議。

そもそも、宝くじをギャンブルとして考えた時、こんな割の合わないギャンブルもないと言われています。
日本にある競馬やパチンコといったギャンブルには、必ず「胴元」がいて、「テラ銭」を抜かれます。
競馬の場合だと25%、パチンコでは20%が、それぞれ胴元=主催者やパチンコ店の取り分となります。
100円の馬券を買った場合、25円が主催者に回り、配当される(還元される)のは75円ということです。
では、宝くじはどうかというと、驚くなかれ実に52%ものテラ銭を抜かれているのです。
これを数学的に見てみましょう。
膨大に宝くじを買った時の「1回(枚)当たりの平均的な受取額」=「期待値」を、昨年の年末ジャンボ↑を例に計算(小数第4位以下切り捨)してみると、
40+20+0.99+9.009+10+10+30+30=149.999円
となります。
やはり約50%の還元率と同様の結果です。
つまり、年末ジャンボを300円払って購入することは、1回平均で見れば約150円の賞金を得ようとする行為と同じなのです。
もちろん、みなさんおわかりのように、ことはそう単純なものではありません。
それはなぜかというと、賞金が150円という一定額ではないからです。
しかし、いかなるギャンブルも上記の通り胴元がテラ銭を抜くので、賞金の期待値というのは参加料よりも小さくなるものなのです。

ここで、ちょっとみなさんに次のようなゲーム(くじ)について考えてもらいましょう。
公平なコインを、表が出るまで投げ続けます。
表が出たらゲームは終わりで、表が出たのが1回目ならば20円、2回目ならば40円、3回目ならば80円というように、賞金額が1回投げる毎に倍になっていくゲームです。
あなたはこのゲームに、いくらまでならお金を払って参加しますか?
私は、「3回くらいなら続けて裏が出るかもしれないので、80円なら参加するかな?」と思いました。
しかしこれ、数学的にみると、1000万円でも1億円でも払って参加するべし!!というのが解答なのだそうです。
詳しい解説は避けますが、このゲームでは上述の「期待値」 が無限大なので、いくら払ってでも参加するべきなのだとか。
もちろん、誰もそんなお金を払って参加しようなどとは思いませんよね。
では、なぜ期待値が投資額の半分でしかない(マイナスの)宝くじは買うのに、期待値が無限大のこのくじには参加しないのでしょう…
これは「ベルヌーイの定理」で有名な、18世紀の数学者ダニエル・ベルヌイが考案した『セント・ペテルスブルグのパラドックス』と呼ばれるものです。

なぜ人はこのように期待値基準に背いてしまうのでしょう?
これには「確率」に対する感覚の歪みと、「賞金」に対する感覚の歪みの2つがあると言います。
これに対しても詳しい解説は避けますが、結論を言うと『人は確率や賞金額ではなく、それがもたらす「嬉しさ」を基準に判断している』ということなのです。
「射幸心」とも言いますが、「自分に1回だけものすごい幸運が訪れ、人生を劇的に変えてくれる」ことを期待して買うわけです。
これを可能にしているのが「お金の還付に変動性がある」ことです。

数億円という1等の当選金は、およそ庶民にとって人生を大きく変えるだろう金額であり、「射幸心を煽る」には十分なわけで、人は確率や期待値など関係なく買ってしまうと言うわけです。
これの裏返しが、上述のベルヌーイのパラドクスで、その人の持つ財産との関係によって、賭けるお金の値うちが違うということが、数学的な期待値の定義では無視されたのでパラドクスが生じたと結論づけています。
賭けの期待金額は無限大でも、参加者が賞金を受け取った時の「嬉しさ」の度合いは無限大ではないというわけです。

ここで、これまた有名な17世紀フランスの哲学者であり、神学者であり、数学者でもある、現在はその名が圧力の国際単位にもなっているパスカルの考案を紹介してみます。
パスカルは期待効用というものを用いて「神の存在証明」を行ったことでも有名です。
それによると…
これを宝くじに置き換えてみてはどうでしょう?
宝くじの高額当選の確率が極めて低くてもゼロではなく、ハズれてもマイナスは有限です。
しかし、買わなければゼロです。
だから、宝くじを買うべきだ。
と受け取ることもできるわけです。
確率や期待値だけを考えれば、宝くじに限らずギャンブルというものは、確実に損をすることになっています。
しかし、たった一度の短い人生の中では集計自体が意味をもたないわけで、「二度とない次のチャンス」に賭けることは決して無駄なことではないようです。
というわけで、長々と宝くじについて書いてきたわけですが、実はこれ、最近読んだ『数学的決断の技術』(小島寛之著:朝日新書)から多くを引用しています。
本の中ではもっと詳しく解説してくれていますので、興味のある方は是非ご覧になってみてください。

さて、私ですが、宝くじを買うことが、数学的にも合理的なことだと理解できました。
懐の許す範囲で…という条件付きではありますが、これで、「確率が…」だの、「還付率が…」だのと考えることなく、胸を張って夢を追い続けることができそうです。
…ま、当たんないけどね。

戦歴はと言えば、遠い昔に、たぶん3千円程度当たったような気もしないではないのですが、それも定かではありません。
そんな「確実に当たらない」宝くじなのに、なぜ買い続けているのでしょうか?
今日は、こうも当たらない宝くじについて、冷静に考えてみたいと思います。
ちょっと長くなりそうですので、興味のない方は斜め読みでどうぞ。

さて、宝くじの当選確率って一体どれくらいのものなのでしょう?
宝くじは買っているのに、果たして1等の当選確率がどれほどのものか、案外知らない方も多いのではないでしょうか。
年に5回あるジャンボ宝くじの1等当選確率は、なんと1000万分の1です。

1000万個の球の入った抽選器(ガラガラ)の中に、たった1個の1等の球が入っていることを考えると、これがいかに確率の低いものかおわかりになるかと思います。
よりわかりやすくするために、ガラガラの球の直径が1cmとして計算すると、ぎっしりと球を積んだ10tダンプ約35台分の中に1個という割合です。

一列に並べたら、その距離実に100kmにも及びます。
こんなの当たるわけないよなぁ、という気になってきますよね。
しかし、「1等60本」だとか、「毎回○○名の億万長者が誕生」とかいうCMを見聞きしていると、「…きっと自分も当たるのでは?」という気になってくるから不思議。

そもそも、宝くじをギャンブルとして考えた時、こんな割の合わないギャンブルもないと言われています。
日本にある競馬やパチンコといったギャンブルには、必ず「胴元」がいて、「テラ銭」を抜かれます。
競馬の場合だと25%、パチンコでは20%が、それぞれ胴元=主催者やパチンコ店の取り分となります。
100円の馬券を買った場合、25円が主催者に回り、配当される(還元される)のは75円ということです。
では、宝くじはどうかというと、驚くなかれ実に52%ものテラ銭を抜かれているのです。
これを数学的に見てみましょう。
膨大に宝くじを買った時の「1回(枚)当たりの平均的な受取額」=「期待値」を、昨年の年末ジャンボ↑を例に計算(小数第4位以下切り捨)してみると、
40+20+0.99+9.009+10+10+30+30=149.999円
となります。
やはり約50%の還元率と同様の結果です。
つまり、年末ジャンボを300円払って購入することは、1回平均で見れば約150円の賞金を得ようとする行為と同じなのです。
もちろん、みなさんおわかりのように、ことはそう単純なものではありません。
それはなぜかというと、賞金が150円という一定額ではないからです。
しかし、いかなるギャンブルも上記の通り胴元がテラ銭を抜くので、賞金の期待値というのは参加料よりも小さくなるものなのです。

ここで、ちょっとみなさんに次のようなゲーム(くじ)について考えてもらいましょう。
公平なコインを、表が出るまで投げ続けます。
表が出たらゲームは終わりで、表が出たのが1回目ならば20円、2回目ならば40円、3回目ならば80円というように、賞金額が1回投げる毎に倍になっていくゲームです。
あなたはこのゲームに、いくらまでならお金を払って参加しますか?
私は、「3回くらいなら続けて裏が出るかもしれないので、80円なら参加するかな?」と思いました。
しかしこれ、数学的にみると、1000万円でも1億円でも払って参加するべし!!というのが解答なのだそうです。
詳しい解説は避けますが、このゲームでは上述の「期待値」 が無限大なので、いくら払ってでも参加するべきなのだとか。
もちろん、誰もそんなお金を払って参加しようなどとは思いませんよね。
では、なぜ期待値が投資額の半分でしかない(マイナスの)宝くじは買うのに、期待値が無限大のこのくじには参加しないのでしょう…
これは「ベルヌーイの定理」で有名な、18世紀の数学者ダニエル・ベルヌイが考案した『セント・ペテルスブルグのパラドックス』と呼ばれるものです。

なぜ人はこのように期待値基準に背いてしまうのでしょう?
これには「確率」に対する感覚の歪みと、「賞金」に対する感覚の歪みの2つがあると言います。
これに対しても詳しい解説は避けますが、結論を言うと『人は確率や賞金額ではなく、それがもたらす「嬉しさ」を基準に判断している』ということなのです。
「射幸心」とも言いますが、「自分に1回だけものすごい幸運が訪れ、人生を劇的に変えてくれる」ことを期待して買うわけです。
これを可能にしているのが「お金の還付に変動性がある」ことです。

数億円という1等の当選金は、およそ庶民にとって人生を大きく変えるだろう金額であり、「射幸心を煽る」には十分なわけで、人は確率や期待値など関係なく買ってしまうと言うわけです。
これの裏返しが、上述のベルヌーイのパラドクスで、その人の持つ財産との関係によって、賭けるお金の値うちが違うということが、数学的な期待値の定義では無視されたのでパラドクスが生じたと結論づけています。
賭けの期待金額は無限大でも、参加者が賞金を受け取った時の「嬉しさ」の度合いは無限大ではないというわけです。

ここで、これまた有名な17世紀フランスの哲学者であり、神学者であり、数学者でもある、現在はその名が圧力の国際単位にもなっているパスカルの考案を紹介してみます。
パスカルは期待効用というものを用いて「神の存在証明」を行ったことでも有名です。
それによると…
神が存在する確率が極めて低くても、それはゼロとは言えない。
そして、神が存在した場合の効用は無限大である。
仮に神の存在に賭けて、それが存在しなかったとしても、その負の効用は有限であろう。
他方、神の存在に賭けなければ、効用はゼロである。
だから、人は神の存在に賭けるべきだ。
これを宝くじに置き換えてみてはどうでしょう?
宝くじの高額当選の確率が極めて低くてもゼロではなく、ハズれてもマイナスは有限です。
しかし、買わなければゼロです。
だから、宝くじを買うべきだ。
と受け取ることもできるわけです。
確率や期待値だけを考えれば、宝くじに限らずギャンブルというものは、確実に損をすることになっています。
しかし、たった一度の短い人生の中では集計自体が意味をもたないわけで、「二度とない次のチャンス」に賭けることは決して無駄なことではないようです。
というわけで、長々と宝くじについて書いてきたわけですが、実はこれ、最近読んだ『数学的決断の技術』(小島寛之著:朝日新書)から多くを引用しています。
本の中ではもっと詳しく解説してくれていますので、興味のある方は是非ご覧になってみてください。
さて、私ですが、宝くじを買うことが、数学的にも合理的なことだと理解できました。
懐の許す範囲で…という条件付きではありますが、これで、「確率が…」だの、「還付率が…」だのと考えることなく、胸を張って夢を追い続けることができそうです。
…ま、当たんないけどね。

コメントフォーム















